1. Den Biegeprozess verstehen: einfache Fakten
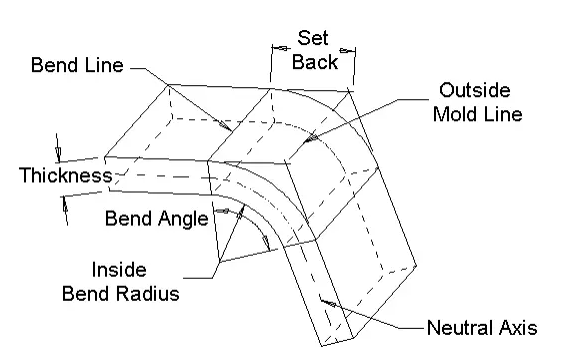
Biegezugabe = Winkel * (T/ 180) * (Radius + K-Faktor * Dicke) Biegekompensation = Biegezugabe (2 * Zurücksetzen)
Innenversatz = hellbraun (Winkel / 2) *Radius Außenversatz = hellbraun (Winkel / 2)*(Radius + Dicke)

1) Der an einem gebogenen Teil erhaltene Radius beeinflusst die Länge, auf die wir dieses Teil schneiden müssen (vor dem Biegen).
2) Der beim Biegen erzielte Radius hängt zu 99 % von der V-Öffnung ab, mit der wir arbeiten.
Bevor wir das Teil konstruieren und sicherlich bevor wir mit dem Schneiden der Rohlinge beginnen, MÜSSEN wir GENAU wissen, welche V-Öffnung wir verwenden werden, um das Teil auf der Abkantpresse zu biegen.
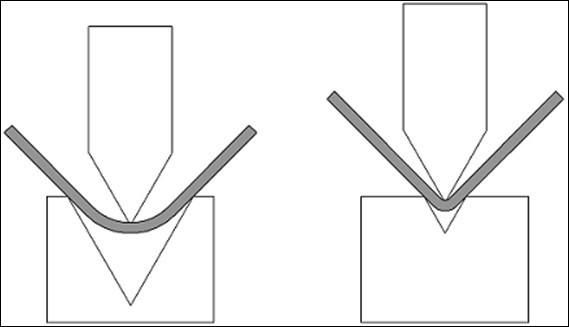
2. Wie sich der Radius auf Rohlinge auswirkt
ein größerer Radius „drückt“ die Beine unseres Teils nach außen und erweckt den Eindruck, dass der Rohling „zu lang“ geschnitten wurde.
Ein kleinerer Radius erfordert einen Rohling, der „etwas länger“ geschnitten werden muss, als wenn der Radius größer wäre.
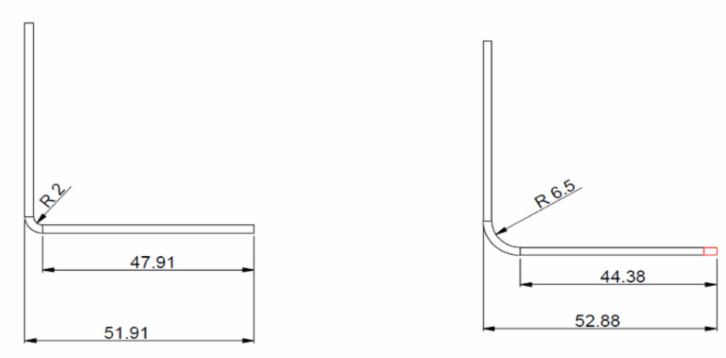
3. Biegezugabe
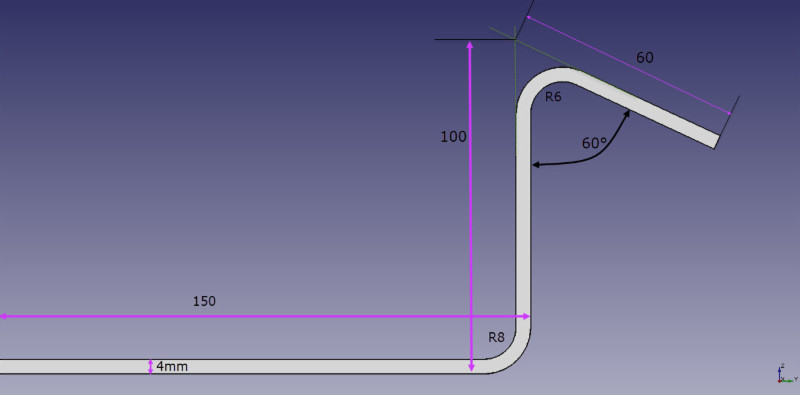
Die ungefalteten Leerzeichen der obigen Abbildung würden wie folgt berechnet:
B = 150 + 100 + 60 + BA1 + BA2
So berechnen Sie BA1 und BA2:
Berechnung der Biegezugabe
Der Teil, den wir von beiden Beinen reduzieren müssen, sobald sie sich überlappen, indem sie flach werden, ist das, was wir allgemein als „Biegezugabe“ (oder BA in der Gleichung) kennen.
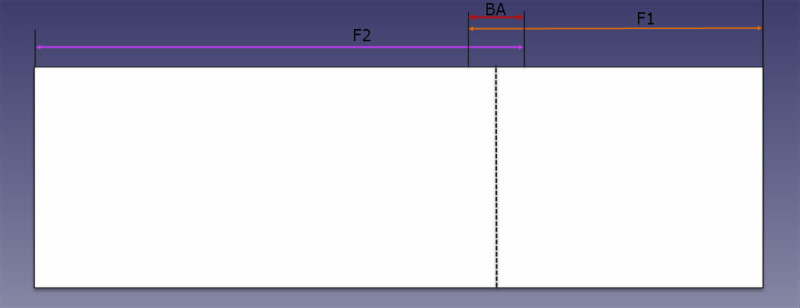
Biegezugabeformel
BA-Formel für Biegungen bis 90°
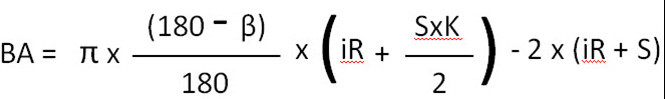
BA-Formel für Biegungen von 91° bis 165°
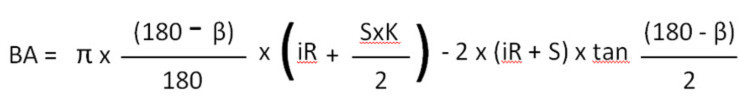
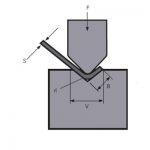
iR= Innenradius
S=Dicke
Β = Winkel
Π = 3,14159265….
K = K-Faktor
K-Faktor
Beim Biegen auf einer Abkantpresse wird der innere Teil des Blechs gestaucht, während der äußere Teil gedehnt wird.
Das bedeutet, dass es einen Teil des Blattes gibt, wo die Fasern weder komprimiert noch gedehnt werden. Wir nennen diesen Teil die „neutrale Achse“.
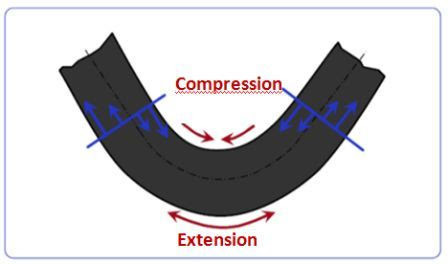
Der Abstand von der Innenseite der Biegung zur neutralen Achse wird als K-Faktor bezeichnet.
Dieser Wert wird mit dem von uns gekauften Material geliefert und kann nicht geändert werden.
Dieser Wert wird in Brüchen ausgedrückt. Je kleiner der K-Faktor ist, desto näher liegt die neutrale Achse am Innenradius des Blechs.
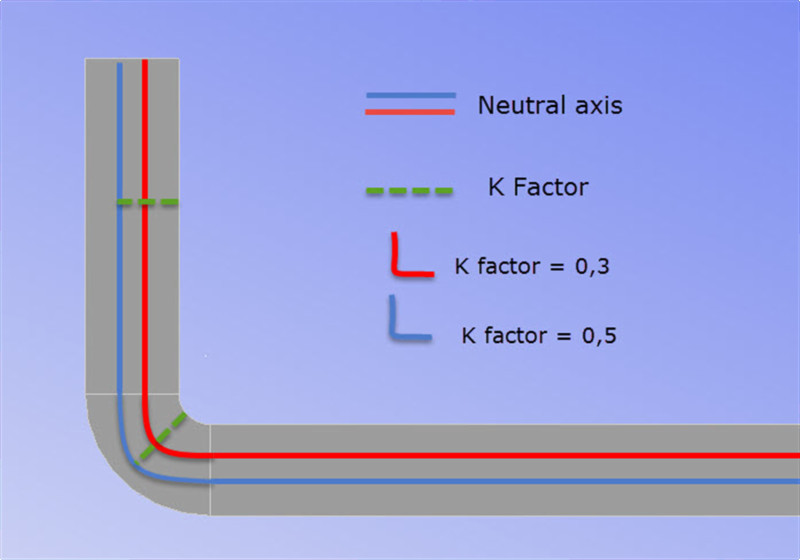
K-Faktor = Feinabstimmung
Der K-Faktor beeinflusst unseren ungefalteten Rohling. Nicht so sehr wie der Radius des Teils, aber wir können es uns als Feinabstimmungsberechnungen für Rohlinge vorstellen.
je kleiner der K-Faktor, desto mehr Material wird gedehnt und somit „herausgedrückt“…. was bedeutet, dass unser Bein „größer“ wird.
Schätzung des K-Faktors
Meistens können wir den K-Faktor bei der Feinabstimmung unserer Rohlingsberechnungen abschätzen und anpassen.
Alles, was wir tun müssen, sind einige Tests (an der gewählten V-Öffnung) und den Radius des Teils zu messen.
Falls Sie einen genaueren K-Faktor bestimmen müssen, finden Sie unten die Berechnung zur Bestimmung des genauen K-Faktors für Ihre Biegung.

K-Faktor: eine Formel
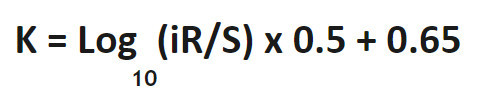
Lösung des Beispiels:
B = 150 + 100 + 60 + BA1 + BA2
K-Faktor-Schätzung
B1: R/S=2 => K=0,8
B2: R/S=1,5 => K=0,8
Beide Biegungen sind 90° oder weniger:
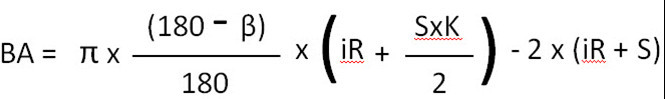
was bedeutet:
B1 = 3,14 x 0,66 x (6 + ((4×0,8)/2) – 2 x 10
B1 = -4,25
B2 = 3,14 x 0,5 x (8 + ((4×0,8)/2) – 2 x 12
B2 = -8,93
deshalb:
B = 150 + 100 + 60 + (-4,25) + (-8,93)
B = 296,8 mm